Floor Function Of Exponential Distribution

Distribution of the exponential of an exponential random variable.

Floor function of exponential distribution.

Deterministic transformations of the. It completes the methods with details specific for this. The exponential distribution is often used to model the longevity of an electrical or mechanical device. In example the lifetime of a certain computer part has the exponential distribution with a mean of ten years x sim exp 0.

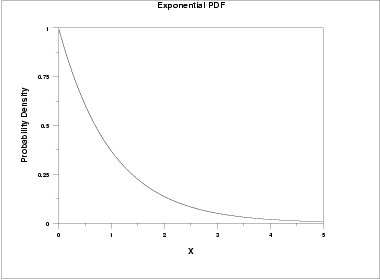
Floor and ceil function python. The above interpretation of the exponential is useful in better understanding the properties of the exponential distribution. The probability density function pdf of an exponential distribution is here λ 0 is the parameter of the distribution often called the rate parameter the distribution is supported on the interval 0. The most important of these properties is that the exponential distribution is memoryless.

Smooth approximation to the floor function. The geometric distribution is a discrete analog of the exponential distribution and is the only discrete distribution with a constant hazard function. Proof that the floor of an exponential random variable is a geometric variable. Definitions probability density function.

Similarly to the box muller transformation which is a method to sample normally distributed random numbers based on a uniform random generator i have found that any probability distribution admits one liners i e. Exponential density in r. How to pop the last positional argument of a bash function or script. I need to sample random numbers distributed according to the geometric distribution.

Python truncated exponential distribution in statistics last updated. Generalized pareto distribution the generalized pareto distribution is a three parameter continuous distribution that has parameters k shape σ scale and θ threshold. Scipy stats truncexpon is a truncated exponential continuous random variable. The exponential distribution exhibits infinite divisibility.

To see this think of an exponential random variable in the sense of tossing a lot of coins until observing the first heads. If a random variable x has this distribution we write x exp λ.